I’ve never considered drawing to be part of my practice, but more recently I’ve come to realise that I do like drawing. It is a tool I use more often than I think – especially when communicating a technique to students or making sense of something I’m making, and even when I’m tutoring maths. In fact the marks I make be they lines, sketches, mathematical symbols or algebraic notation- they could all be categorised as drawing.
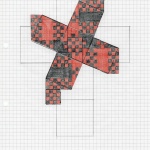
So having woven a 10×10 7,3 closed cube, and being left with some unanswered questions, I decided I should draw the cube as a way of ‘making sense’ of what was going on. I should explain what I mean by a 10×10 7,3 closed cube. To create the skew you must first start with a square, in this case it has dimensions 10×10. The skew in the base of the cube is formed by locating a point on each side of the square. For my first woven skew cube the points were such that four right angled triangles were positioned using the vertices of the 10×10 square being the right angle, each triangle with perpendicular side lengths of 7 and 3.The skew continues and is replicated on each face. The cube is closed with all six faces covered by woven strands.
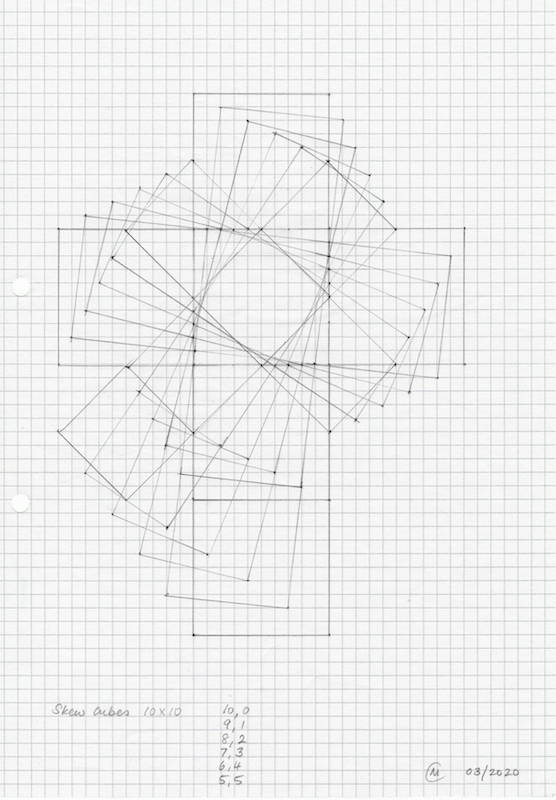
My initial diagram shows how a skew cube net relates to that of a standard cube with sides 10x10x10. I really like the way the nets spiral around the centre of the base.
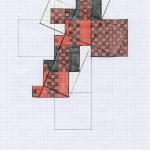
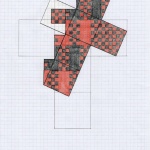
Following diagrams (see the Gallery below) were derived from the 7,3 cube/net and how it could be interpreted. I must admit feeling stumped as to what was happening to the strands in the weaving, in terms of why or how there were some that conflicted. I also very quickly came to realise that colouring individual squares on a diagram detaches from the process of weaving. The woven strands are dynamic, with movement and direction. The coloured squares are static and no longer relate to the strand, their sense of being part of something greater is lost. They are just squares…
All that being said, the process of recording by drawing or ‘diagramming’ was worthwhile. It made me look more closely at the cube, turning it over and around in both hands (it being quite large). The turns taken by the strands were sometimes unexpected, longer than I thought and on occasions the transition from 3D to 2D confusing.
I became really interested in the top face. In the process of weaving the cube and identifying that it had some conflicting strands, I had to set some rules. Non conflicting strands could be over woven as this would not affect the pattern. My rule dictated that conflicting strands met with one strand on the hypotenuse of the triangle and the other running across the top face to meet it.

The top face has rotation symmetry of order two, if you take the two colours into account. Without the colours, if you just look at the lines created by the edges of the strands it has rotational symmetry of order four. The patterns on the triangles were really unexpected, with a reassuring echo of the base shown as a small chequerboard.
The process started to show up some interesting happenings. The two conflicting strands running across the face of the top seemed to originate from the diagonally opposite vertices, one each from two faces, but this needed further investigation.
This post was part of my contribution to the Forces in Translation project it has been shared on this website with the kind permission of the project team.